Chưa có sản phẩm trong giỏ hàng.
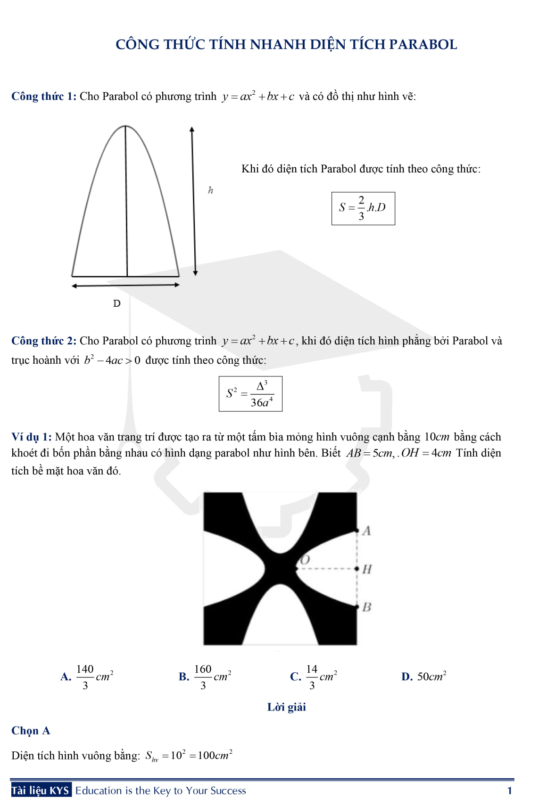
Chào mừng bạn đến với thế giới toán học thú vị và đầy ứng dụng! Hôm nay, chúng ta sẽ cùng nhau khám phá một khái niệm quan trọng và vô cùng hữu ích trong hình học giải tích: **Diện tích parabol**. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về cách tính diện tích parabol, công thức liên quan, ví dụ minh họa dễ hiểu, bài tập thực hành và những ứng dụng thực tế bất ngờ của nó. Hãy cùng Phan Rang Soft khám phá ngay nhé!
Tóm tắt nội dung
Diện tích Parabol: Định nghĩa và Ý nghĩa
Parabol là một đường cong bậc hai, được định nghĩa là tập hợp các điểm cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn). Parabol xuất hiện rất nhiều trong tự nhiên và trong các ứng dụng kỹ thuật, từ quỹ đạo của một quả bóng được ném lên đến hình dạng của gương phản xạ trong đèn pha ô tô.
Diện tích parabol, một cách đơn giản, là diện tích được giới hạn bởi đường cong parabol và một đường thẳng nào đó. Việc tính toán diện tích này không chỉ là một bài toán hình học thuần túy mà còn có ý nghĩa quan trọng trong nhiều lĩnh vực như:
- Kỹ thuật: Tính toán diện tích của các bộ phận máy móc có hình dạng parabol.
- Vật lý: Xác định diện tích dưới đường cong biểu diễn sự thay đổi của một đại lượng vật lý nào đó theo thời gian.
- Toán học ứng dụng: Giải quyết các bài toán tối ưu hóa liên quan đến hình dạng parabol.
Công thức Tính Diện tích Parabol
Để tính diện tích parabol, chúng ta cần xác định được phương trình của parabol và đường thẳng giới hạn. Dưới đây là một số công thức phổ biến:
1. Parabol có dạng y = ax2 và đường thẳng y = b
Trong trường hợp này, parabol có đỉnh tại gốc tọa độ (0,0) và mở lên trên (nếu a > 0) hoặc xuống dưới (nếu a < 0). Đường thẳng y = b là một đường thẳng nằm ngang. Diện tích parabol giới hạn bởi parabol và đường thẳng này được tính theo công thức:
S = (2/3) * b * √(b/a) (nếu a > 0 và b > 0)
Công thức này chỉ áp dụng khi b > 0, tức là đường thẳng y = b nằm phía trên trục hoành.
2. Parabol có dạng y = ax2 + bx + c và đường thẳng y = mx + n
Đây là trường hợp tổng quát hơn. Để tính diện tích parabol trong trường hợp này, chúng ta cần thực hiện các bước sau:
- Tìm giao điểm của parabol và đường thẳng: Giải phương trình ax2 + bx + c = mx + n để tìm ra hai nghiệm x1 và x2.
- Tính tích phân: Diện tích S được tính bằng công thức tích phân:
- S = |∫x1x2 [(mx + n) – (ax2 + bx + c)] dx|
Công thức này có nghĩa là chúng ta tính tích phân của hiệu giữa phương trình đường thẳng và phương trình parabol, lấy cận từ x1 đến x2. Giá trị tuyệt đối đảm bảo rằng diện tích luôn dương.
3. Trường hợp đặc biệt: Parabol cắt trục hoành
Nếu parabol cắt trục hoành tại hai điểm x1 và x2, diện tích parabol giới hạn bởi parabol và trục hoành (y = 0) được tính bằng công thức:
S = |∫x1x2 (ax2 + bx + c) dx|
Trong trường hợp này, chúng ta chỉ cần tính tích phân của phương trình parabol từ x1 đến x2.
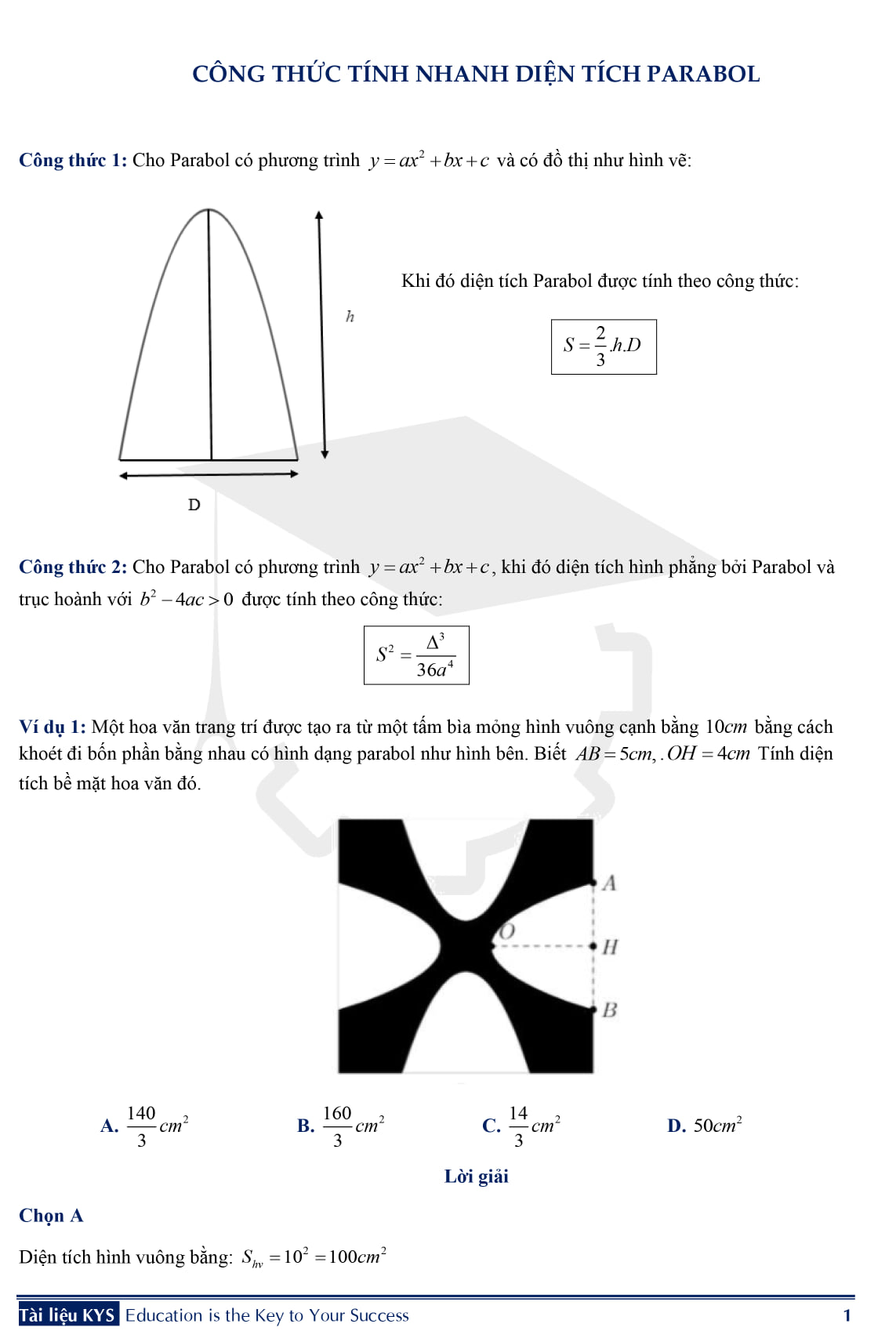
Ví dụ Minh họa
Để hiểu rõ hơn về cách áp dụng các công thức trên, chúng ta hãy cùng xem xét một số ví dụ cụ thể:
Ví dụ 1: Tính diện tích parabol y = x2 và đường thẳng y = 4
Ở đây, a = 1 và b = 4. Áp dụng công thức S = (2/3) * b * √(b/a), ta có:
S = (2/3) * 4 * √(4/1) = (2/3) * 4 * 2 = 16/3
Vậy, diện tích parabol là 16/3 đơn vị diện tích.
Ví dụ 2: Tính diện tích parabol y = x2 – 2x và trục hoành
Đầu tiên, ta tìm giao điểm của parabol và trục hoành bằng cách giải phương trình x2 – 2x = 0. Ta có x(x – 2) = 0, vậy x1 = 0 và x2 = 2.
Tiếp theo, ta tính tích phân:
S = |∫02 (x2 – 2x) dx| = |[x3/3 – x2]02| = |(8/3 – 4) – (0)| = |-4/3| = 4/3
Vậy, diện tích parabol là 4/3 đơn vị diện tích.
Ví dụ 3: Tính diện tích parabol y = x2 và đường thẳng y = x + 2
Tìm giao điểm: x2 = x + 2 => x2 – x – 2 = 0 => (x – 2)(x + 1) = 0 => x1 = -1 và x2 = 2
Tính tích phân:
S = |∫-12 [(x + 2) – x2] dx| = |[x2/2 + 2x – x3/3]-12| = |(2 + 4 – 8/3) – (1/2 – 2 + 1/3)| = |10/3 – (-7/6)| = |27/6| = 9/2
Vậy diện tích là 9/2 đơn vị diện tích
Bài tập Thực hành
Để củng cố kiến thức, bạn hãy thử sức với một số bài tập sau:
- Tính diện tích parabol y = 2x2 và đường thẳng y = 8.
- Tính diện tích parabol y = -x2 + 4x và trục hoành.
- Tính diện tích parabol y = x2 + 1 và đường thẳng y = 2x + 2.
Bạn có thể kiểm tra đáp án của mình bằng cách sử dụng các công cụ tính toán trực tuyến hoặc tham khảo các tài liệu toán học khác.
Ứng dụng của Diện tích Parabol
Diện tích parabol không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Thiết kế kiến trúc: Parabol được sử dụng để thiết kế các mái vòm, cầu treo và các công trình kiến trúc khác. Việc tính toán diện tích parabol giúp đảm bảo tính ổn định và hiệu quả của các công trình này.
- Quang học: Gương parabol được sử dụng trong các kính thiên văn, kính hiển vi và các thiết bị quang học khác. Diện tích parabol ảnh hưởng đến khả năng thu thập và tập trung ánh sáng của các thiết bị này.
- Cơ học: Quỹ đạo của một vật thể được ném lên trong không gian (bỏ qua sức cản của không khí) có dạng parabol. Việc tính toán diện tích dưới đường cong quỹ đạo giúp xác định các thông số quan trọng như tầm xa và thời gian bay của vật thể.
Như vậy, kiến thức về diện tích parabol không chỉ giúp bạn giải quyết các bài toán hình học mà còn mở ra cánh cửa khám phá những ứng dụng thú vị trong thế giới xung quanh.
Nếu bạn quan tâm đến các chủ đề giáo dục khác, hãy xem thêm các bài viết hữu ích khác trên website Phan Rang Soft.
Kết luận
Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về **diện tích parabol**, từ định nghĩa, công thức tính toán đến ví dụ minh họa và ứng dụng thực tế. Hãy nhớ rằng, toán học không chỉ là những con số khô khan mà còn là một công cụ mạnh mẽ để khám phá và giải quyết các vấn đề trong cuộc sống.
Đừng ngần ngại liên hệ với chúng tôi nếu bạn có bất kỳ thắc mắc nào hoặc muốn tìm hiểu thêm về các dịch vụ và sản phẩm của Phan Rang Soft.
Thông tin liên hệ:
Hotline: 0865.427.637
Zalo: https://zalo.me/0865427637
Email: phanrangninhthuansoft@gmail.com
Pinterest: https://in.pinterest.com/phanrangsoftvn/
Facebook: https://www.facebook.com/phanrangsoft/
Website: https://phanrangsoft.com/