Blog, Giáo dục

Diện tích hình tam giác – Cách tính, công thức và ứng dụng, đầy đủ

Posted on by vantuongthang
Diện tích hình tam giác
19
Th7

Chào mừng bạn đến với thế giới hình học thú vị! Trong bài viết này, chúng ta sẽ cùng nhau khám phá một khái niệm cơ bản nhưng vô cùng quan trọng: Diện tích hình tam giác. Đặc biệt, chúng ta sẽ tìm hiểu về cách tính, công thức, ví dụ minh họa, bài tập áp dụng và những ứng dụng thực tế của nó. Hãy cùng Phan Rang Soft khám phá tri thức nhé!

Diện tích hình tam giác: Khái niệm cơ bản

Hình tam giác là một hình đa giác có ba cạnh và ba góc. Việc tính diện tích hình tam giác là một trong những bài toán cơ bản nhất trong hình học, và nó có rất nhiều ứng dụng trong cuộc sống hàng ngày cũng như trong các lĩnh vực khoa học kỹ thuật.

Diện tích hình tam giác là phần không gian bên trong giới hạn bởi ba cạnh của tam giác đó. Đơn vị đo diện tích thường là mét vuông (m²), centimet vuông (cm²), hoặc các đơn vị tương tự.

Diện tích hình tam giác
Diện tích hình tam giác

Các công thức tính diện tích hình tam giác phổ biến

Có nhiều công thức khác nhau để tính diện tích hình tam giác, tùy thuộc vào thông tin mà chúng ta có. Dưới đây là một số công thức phổ biến nhất:

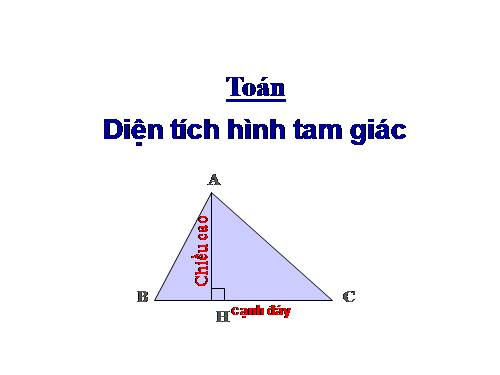
    1. Công thức 1: Diện tích hình tam giác khi biết chiều cao và cạnh đáy

Đây là công thức cơ bản nhất để tính diện tích hình tam giác. Nếu chúng ta biết chiều cao (h) và cạnh đáy (b) của tam giác, thì diện tích (A) được tính theo công thức:

A = (1/2) * b * h

Trong đó:

      • A: Diện tích hình tam giác
      • b: Độ dài cạnh đáy
      • h: Chiều cao tương ứng với cạnh đáy đó
    2. Công thức 2: Diện tích hình tam giác khi biết độ dài ba cạnh (Công thức Heron)

Khi chúng ta biết độ dài ba cạnh của tam giác (a, b, c), chúng ta có thể sử dụng công thức Heron để tính diện tích. Công thức này như sau:

A = √(s * (s – a) * (s – b) * (s – c))

Trong đó:

      • A: Diện tích hình tam giác
      • a, b, c: Độ dài ba cạnh của tam giác
      • s: Nửa chu vi của tam giác, được tính bằng: s = (a + b + c) / 2
    2. Công thức 3: Diện tích hình tam giác khi biết hai cạnh và góc xen giữa

Nếu chúng ta biết độ dài hai cạnh của tam giác (a, b) và góc xen giữa hai cạnh đó (γ), chúng ta có thể sử dụng công thức sau:

A = (1/2) * a * b * sin(γ)

Trong đó:

      • A: Diện tích hình tam giác
      • a, b: Độ dài hai cạnh của tam giác
      • γ: Góc xen giữa hai cạnh a và b
    2. Công thức 4: Diện tích hình tam giác vuông

Tam giác vuông là tam giác có một góc vuông (90 độ). Diện tích tam giác vuông được tính bằng công thức:

A = (1/2) * a * b

Trong đó:

    • A: Diện tích hình tam giác vuông
    • a, b: Độ dài hai cạnh góc vuông

Ví dụ minh họa cách tính diện tích hình tam giác

Để hiểu rõ hơn về cách áp dụng các công thức trên, chúng ta hãy cùng xem xét một vài ví dụ minh họa:

    • Ví dụ 1: Cho một tam giác có cạnh đáy là 10 cm và chiều cao tương ứng là 5 cm. Tính diện tích của tam giác này.

Áp dụng công thức A = (1/2) * b * h, ta có:

A = (1/2) * 10 cm * 5 cm = 25 cm²

Vậy diện tích của tam giác là 25 cm².

    • Ví dụ 2: Cho một tam giác có độ dài ba cạnh lần lượt là 3 cm, 4 cm và 5 cm. Tính diện tích của tam giác này.

Áp dụng công thức Heron, ta có:

s = (3 + 4 + 5) / 2 = 6 cm

A = √(6 * (6 – 3) * (6 – 4) * (6 – 5)) = √(6 * 3 * 2 * 1) = √36 = 6 cm²

Vậy diện tích của tam giác là 6 cm².

    • Ví dụ 3: Cho một tam giác có hai cạnh lần lượt là 6 cm và 8 cm, và góc xen giữa hai cạnh đó là 30 độ. Tính diện tích của tam giác này.

Áp dụng công thức A = (1/2) * a * b * sin(γ), ta có:

A = (1/2) * 6 cm * 8 cm * sin(30°) = (1/2) * 6 cm * 8 cm * (1/2) = 12 cm²

Vậy diện tích của tam giác là 12 cm².

Bài tập áp dụng tính diện tích hình tam giác

Để củng cố kiến thức, hãy cùng làm một số bài tập sau:

  1. Một tam giác có cạnh đáy là 12 cm và chiều cao tương ứng là 7 cm. Tính diện tích của tam giác đó.
  2. Một tam giác có độ dài ba cạnh lần lượt là 5 cm, 12 cm và 13 cm. Tính diện tích của tam giác đó.
  3. Một tam giác có hai cạnh lần lượt là 10 cm và 15 cm, và góc xen giữa hai cạnh đó là 45 độ. Tính diện tích của tam giác đó.
  4. Một tam giác vuông có hai cạnh góc vuông lần lượt là 8 cm và 6 cm. Tính diện tích của tam giác vuông đó.

Bạn có thể tìm thấy thêm nhiều bài tập và tài liệu liên quan đến hình học tại Phan Rang Soft, đặc biệt là trong chuyên mục giáo dục. Xem thêm tại đây để nâng cao kiến thức của mình!

Ứng dụng thực tế của diện tích hình tam giác

Việc tính diện tích hình tam giác không chỉ là một bài toán trong sách giáo khoa, mà còn có rất nhiều ứng dụng trong thực tế, bao gồm:

  • Xây dựng và kiến trúc: Tính diện tích mái nhà, vách tường, hoặc các chi tiết trang trí hình tam giác.
  • Thiết kế đồ họa: Sử dụng trong việc tạo ra các hình ảnh, biểu tượng, hoặc logo có hình tam giác.
  • Địa lý và trắc địa: Tính diện tích các khu vực địa lý có hình dạng gần giống tam giác.
  • Kỹ thuật cơ khí: Tính diện tích bề mặt các chi tiết máy có hình tam giác.
  • May mặc: Tính diện tích các mảnh vải hình tam giác để cắt may quần áo.

Như vậy, việc nắm vững kiến thức về diện tích hình tam giác không chỉ giúp chúng ta giải quyết các bài toán hình học, mà còn có thể áp dụng vào nhiều lĩnh vực khác nhau trong cuộc sống.

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về diện tích hình tam giác. Chúc bạn học tập và làm việc hiệu quả!

Thông tin liên hệ:

Hotline: 0865.427.637

Zalo: https://zalo.me/0865427637

Email: phanrangninhthuansoft@gmail.com

Pinterest: https://in.pinterest.com/phanrangsoftvn/

Facebook: https://www.facebook.com/phanrangsoft/

X: https://x.com/phanrangsoft

Website: https://phanrangsoft.com/