Diện tích hình elip giới hạn bởi - Cách tính, công thức và ứng dụng, đầy đủ

Chào mừng bạn đến với thế giới hình học thú vị! Trong bài viết hôm nay, chúng ta sẽ cùng nhau khám phá một hình dạng quen thuộc nhưng không kém phần hấp dẫn: hình elip. Đặc biệt, chúng ta sẽ đi sâu vào diện tích hình elip, cách tính toán, công thức, ví dụ minh họa, bài tập áp dụng và những ứng dụng thực tế của nó. Hãy cùng Phan Rang Soft khám phá những điều thú vị về hình elip nhé!

Tóm tắt nội dung

Khái niệm về Hình Elip

Trước khi đi vào cách tính diện tích hình elip, chúng ta cần hiểu rõ về hình dạng này. Elip là một đường cong kín, được định nghĩa là tập hợp các điểm mà tổng khoảng cách từ mỗi điểm đến hai điểm cố định (gọi là tiêu điểm) là một hằng số. Elip có hai trục đối xứng: trục lớn (đường kính dài nhất) và trục bé (đường kính ngắn nhất).

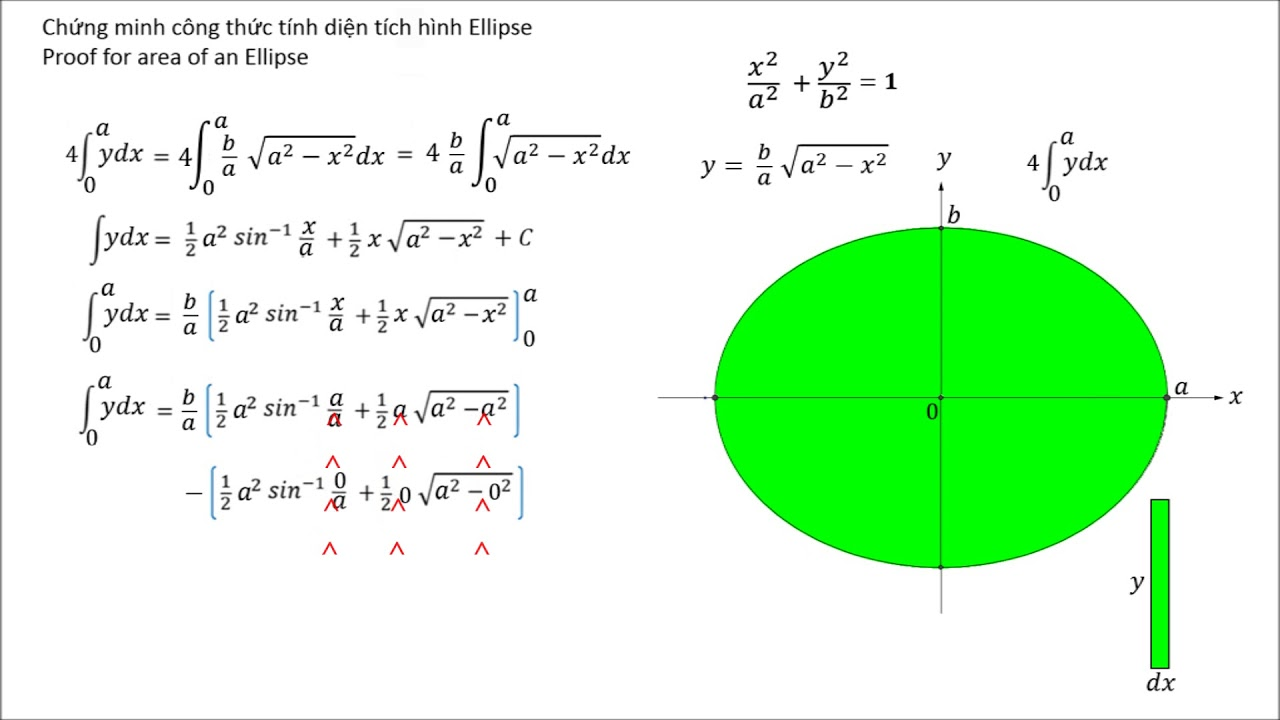
Các Yếu Tố Quan Trọng Của Hình Elip

Để hiểu rõ hơn về hình elip và diện tích hình elip, chúng ta cần nắm vững các yếu tố sau:

Tiêu điểm (F1, F2): Hai điểm cố định dùng để định nghĩa hình elip.
Trục lớn (2a): Đoạn thẳng đi qua hai tiêu điểm và có hai đầu mút nằm trên elip. Nửa trục lớn là ‘a’.
Trục bé (2b): Đoạn thẳng vuông góc với trục lớn, đi qua tâm của elip và có hai đầu mút nằm trên elip. Nửa trục bé là ‘b’.
Tâm (O): Giao điểm của trục lớn và trục bé.
Độ dài tiêu cự (2c): Khoảng cách giữa hai tiêu điểm.

Công Thức Tính Diện Tích Hình Elip

Và bây giờ, chúng ta đến với phần quan trọng nhất: công thức tính diện tích hình elip. Công thức này khá đơn giản và dễ nhớ:

Diện tích hình elip (S) = π * a * b

Trong đó:

π (pi) là một hằng số xấp xỉ bằng 3.14159
a là độ dài nửa trục lớn
b là độ dài nửa trục bé

Ví Dụ Minh Họa Tính Diện Tích Hình Elip

Để giúp bạn hiểu rõ hơn về cách tính diện tích hình elip, chúng ta hãy cùng xem xét một ví dụ cụ thể:

Ví dụ 1: Một hình elip có độ dài nửa trục lớn (a) là 5cm và độ dài nửa trục bé (b) là 3cm. Hãy tính diện tích của hình elip này.

Giải:

Áp dụng công thức: S = π * a * b

S = 3.14159 * 5 * 3

S ≈ 47.12 cm²

Vậy, diện tích của hình elip này xấp xỉ 47.12 cm².

Ví dụ 2: Cho một hình elip có trục lớn bằng 10cm và trục bé bằng 6cm. Tính diện tích hình elip đó.

Giải:

Đầu tiên, ta cần tìm nửa trục lớn (a) và nửa trục bé (b):

a = (trục lớn) / 2 = 10cm / 2 = 5cm
b = (trục bé) / 2 = 6cm / 2 = 3cm

Sau đó, áp dụng công thức tính diện tích hình elip:

S = π * a * b

S = 3.14159 * 5 * 3

S ≈ 47.12 cm²

Vậy, diện tích của hình elip này xấp xỉ 47.12 cm².

Bài Tập Vận Dụng Tính Diện Tích Hình Elip

Để củng cố kiến thức về diện tích hình elip, hãy thử sức với một vài bài tập sau đây:

Một hình elip có nửa trục lớn là 8cm và diện tích là 100cm². Hãy tính độ dài nửa trục bé của hình elip.
Một hình elip có trục lớn là 12cm và trục bé là 8cm. Tính diện tích của hình elip này.
Một sân vận động có hình elip với trục lớn là 100m và trục bé là 60m. Tính diện tích của sân vận động.

Ứng Dụng Thực Tế Của Hình Elip

Hình elip không chỉ là một khái niệm trừu tượng trong toán học. Nó còn có rất nhiều ứng dụng thực tế trong cuộc sống và khoa học kỹ thuật:

Thiên văn học: Quỹ đạo của các hành tinh quanh Mặt Trời có dạng hình elip.
Kiến trúc: Nhiều công trình kiến trúc sử dụng hình elip để tạo ra những không gian độc đáo và ấn tượng.
Vật lý: Hình elip được sử dụng trong các thiết kế quang học, ví dụ như gương elip trong các kính thiên văn.
Y học: Máy tán sỏi sử dụng sóng xung kích hội tụ tại một tiêu điểm của elip để phá vỡ sỏi thận.
Thiết kế: Hình elip được sử dụng rộng rãi trong thiết kế đồ họa, logo, và các sản phẩm công nghiệp.

Ví dụ, trong lĩnh vực thiên văn học, việc hiểu rõ về diện tích hình elip giúp các nhà khoa học tính toán chính xác hơn quỹ đạo của các hành tinh và dự đoán các hiện tượng thiên văn. Xem thêm nhiều kiến thức bổ ích khác tại Phan Rang Soft.

Kết Luận

Vậy là chúng ta đã cùng nhau khám phá diện tích hình elip, từ định nghĩa, công thức tính toán, ví dụ minh họa, bài tập áp dụng, cho đến những ứng dụng thực tế của nó. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về hình dạng thú vị này và có thể áp dụng kiến thức này vào thực tế.

Nếu bạn có bất kỳ câu hỏi nào hoặc muốn tìm hiểu thêm về các chủ đề toán học khác, đừng ngần ngại liên hệ với chúng tôi tại Phan Rang Soft. Chúng tôi luôn sẵn sàng hỗ trợ bạn trên con đường chinh phục tri thức!

Thông tin liên hệ:

Hotline: 0865.427.637

Zalo: https://zalo.me/0865427637

Email: phanrangninhthuansoft@gmail.com

Pinterest: https://in.pinterest.com/phanrangsoftvn/

Facebook: https://www.facebook.com/phanrangsoft/

X: https://x.com/phanrangsoft

Website: https://phanrangsoft.com/