Chưa có sản phẩm trong giỏ hàng.
Chào mừng các bạn học sinh lớp 12 đến với bài viết chi tiết về công thức tính mốt trong chương trình Toán học. Mốt là một khái niệm quan trọng trong thống kê, giúp chúng ta nhận biết giá trị xuất hiện nhiều nhất trong một tập dữ liệu. Trong bài viết này, Phan Rang Soft (phanrangsoft.com) sẽ cùng bạn khám phá công thức, cách tính, ví dụ minh họa, bài tập áp dụng và những ứng dụng thực tế của mốt, giúp bạn nắm vững kiến thức và tự tin chinh phục các bài toán liên quan.
Tóm tắt nội dung
1. Mốt Là Gì? Tại Sao Cần Học Về Mốt?
Trước khi đi sâu vào công thức tính mốt, chúng ta cần hiểu rõ khái niệm cơ bản về mốt. Trong thống kê, mốt (ký hiệu Mo) là giá trị xuất hiện nhiều lần nhất trong một tập dữ liệu. Nói cách khác, nó là giá trị có tần số lớn nhất. Việc hiểu và tính toán được mốt có nhiều ứng dụng quan trọng trong thực tế, chẳng hạn như:
- Phân tích thị trường: Xác định sản phẩm được ưa chuộng nhất, xu hướng tiêu dùng phổ biến.
- Nghiên cứu khoa học: Tìm hiểu đặc điểm chung của một nhóm đối tượng nghiên cứu.
- Quản lý sản xuất: Tối ưu hóa quy trình sản xuất dựa trên nhu cầu thị trường.
- Dự báo: Đưa ra các dự đoán về xu hướng trong tương lai.
Như vậy, việc nắm vững kiến thức về mốt không chỉ giúp bạn đạt điểm cao trong các bài kiểm tra mà còn trang bị cho bạn những kỹ năng cần thiết để phân tích và giải quyết các vấn đề thực tế.
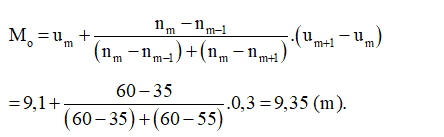
2. Công Thức Tính Mốt (Mo) Cho Dữ Liệu Ghép Nhóm
Khi dữ liệu được cho dưới dạng bảng phân phối tần số (dữ liệu ghép nhóm), việc tính mốt trở nên phức tạp hơn một chút. Chúng ta cần sử dụng công thức tính mốt cho dữ liệu ghép nhóm như sau:
Mo = L + (fm – fm-1) / [(fm – fm-1) + (fm – fm+1)] * h
Trong đó:
- Mo: Mốt của mẫu số liệu.
- L: Giới hạn dưới của lớp chứa mốt (lớp có tần số lớn nhất).
- fm: Tần số của lớp chứa mốt.
- fm-1: Tần số của lớp liền trước lớp chứa mốt.
- fm+1: Tần số của lớp liền sau lớp chứa mốt.
- h: Độ dài của lớp chứa mốt (khoảng cách giữa giới hạn trên và giới hạn dưới của lớp).
Để hiểu rõ hơn về công thức tính mốt này, chúng ta hãy cùng xem xét một ví dụ cụ thể.
3. Ví Dụ Minh Họa Cách Tính Mốt Cho Dữ Liệu Ghép Nhóm
Ví dụ: Cho bảng phân phối tần số về chiều cao của một nhóm học sinh như sau:
| Chiều cao (cm) | Số học sinh |
|---|---|
| 150 – 155 | 5 |
| 155 – 160 | 12 |
| 160 – 165 | 18 |
| 165 – 170 | 10 |
| 170 – 175 | 5 |
Yêu cầu: Tính mốt của mẫu số liệu trên.
Giải:
- Xác định lớp chứa mốt: Lớp chứa mốt là lớp có tần số lớn nhất, trong trường hợp này là lớp 160 – 165 với tần số 18.
- Xác định các giá trị:
- L = 160 (giới hạn dưới của lớp chứa mốt)
- fm = 18 (tần số của lớp chứa mốt)
- fm-1 = 12 (tần số của lớp liền trước lớp chứa mốt)
- fm+1 = 10 (tần số của lớp liền sau lớp chứa mốt)
- h = 5 (độ dài của lớp chứa mốt)
- Áp dụng công thức:Mo = 160 + (18 – 12) / [(18 – 12) + (18 – 10)] * 5Mo = 160 + 6 / (6 + 8) * 5Mo = 160 + 6 / 14 * 5
Mo = 160 + 2.14
Mo ≈ 162.14
Vậy, mốt của chiều cao của nhóm học sinh là khoảng 162.14 cm.
4. Bài Tập Vận Dụng Công Thức Tính Mốt
Để củng cố kiến thức, hãy cùng làm một số bài tập vận dụng về công thức tính mốt:
Bài 1: Cho bảng phân phối tần số về số lượng sản phẩm bán được trong một tháng của một cửa hàng như sau:
| Số lượng sản phẩm | Số tháng |
|---|---|
| 0 – 50 | 3 |
| 50 – 100 | 8 |
| 100 – 150 | 12 |
| 150 – 200 | 7 |
Tính mốt của số lượng sản phẩm bán được.
Bài 2: Điều tra về tuổi của một nhóm người, kết quả thu được như sau:
| Tuổi | Số người |
|---|---|
| 20 – 30 | 10 |
| 30 – 40 | 15 |
| 40 – 50 | 20 |
| 50 – 60 | 12 |
| 60 – 70 | 8 |
Tính mốt của tuổi của nhóm người này.
Bạn có thể tự giải các bài tập này và so sánh kết quả với đáp án để kiểm tra mức độ hiểu bài của mình. Nếu gặp khó khăn, hãy xem lại phần lý thuyết và ví dụ minh họa ở trên.
5. Ứng Dụng Thực Tế Của Mốt
Như đã đề cập ở trên, mốt có nhiều ứng dụng quan trọng trong thực tế. Dưới đây là một số ví dụ cụ thể:
- Trong kinh doanh: Các nhà bán lẻ sử dụng mốt để xác định sản phẩm nào đang bán chạy nhất, từ đó điều chỉnh lượng hàng tồn kho và chiến lược marketing. Ví dụ, một cửa hàng quần áo có thể nhận thấy rằng cỡ áo M được bán nhiều nhất, do đó họ sẽ nhập nhiều áo cỡ M hơn các cỡ khác.
- Trong y học: Các nhà nghiên cứu sử dụng mốt để xác định độ tuổi phổ biến nhất mắc một bệnh nào đó, từ đó tập trung các biện pháp phòng ngừa và điều trị vào nhóm tuổi này. Ví dụ, nếu nghiên cứu cho thấy độ tuổi phổ biến nhất mắc bệnh tim mạch là 55-65 tuổi, các chương trình sàng lọc và giáo dục sức khỏe có thể tập trung vào nhóm tuổi này.
- Trong giáo dục: Các nhà giáo dục có thể sử dụng mốt để xác định mức độ phổ biến của một lỗi sai nào đó trong bài làm của học sinh, từ đó tập trung vào việc giảng dạy và sửa lỗi cho học sinh. Ví dụ, nếu nhiều học sinh mắc lỗi sai khi giải một bài toán về công thức tính mốt, giáo viên cần dành thêm thời gian để giải thích và luyện tập về chủ đề này.
Thông qua những ứng dụng này, chúng ta thấy rằng mốt là một công cụ thống kê hữu ích, giúp chúng ta đưa ra các quyết định dựa trên dữ liệu và hiểu rõ hơn về thế giới xung quanh.
6. Kết Luận
Trong bài viết này, chúng ta đã tìm hiểu về công thức tính mốt cho dữ liệu ghép nhóm, cách tính, ví dụ minh họa, bài tập áp dụng và những ứng dụng thực tế của mốt. Hy vọng rằng những kiến thức này sẽ giúp bạn tự tin hơn trong việc giải các bài toán thống kê và áp dụng chúng vào cuộc sống.
Nếu bạn muốn tìm hiểu thêm về các kiến thức toán học khác, hãy truy cập website của Phan Rang Soft tại https://phanrangsoft.com/category/giao-duc/ để khám phá nhiều bài viết hữu ích khác. Xem thêm nhiều kiến thức bổ ích khác tại đây!
Chúc các bạn học tập tốt và đạt được nhiều thành công!
Thông tin liên hệ:
Hotline: 0865.427.637
Zalo: https://zalo.me/0865427637
Email: phanrangninhthuansoft@gmail.com
Pinterest: https://in.pinterest.com/phanrangsoftvn/
Facebook: https://www.facebook.com/phanrangsoft/
Website: https://phanrangsoft.com/

