Blog, Giáo dục

Công thức đạo hàm – Đầy đủ, chi tiết

Posted on by vantuongthang
Công thức đạo hàm
18
Th7

Chào mừng bạn đến với thế giới Toán học đầy thú vị tại Phan Rang Soft! Trong bài viết này, chúng ta sẽ cùng nhau khám phá một chủ đề vô cùng quan trọng và hữu ích: **Công thức đạo hàm**. Đây là một trong những nền tảng cơ bản của giải tích, đóng vai trò then chốt trong việc giải quyết nhiều bài toán thực tế, từ vật lý, kỹ thuật cho đến kinh tế. Hãy cùng Phan Rang Soft tìm hiểu chi tiết về chủ đề này nhé!

1. Đạo Hàm Là Gì?

Trước khi đi sâu vào các công thức, chúng ta cần hiểu rõ khái niệm đạo hàm. Về cơ bản, đạo hàm của một hàm số tại một điểm là tốc độ thay đổi tức thời của hàm số đó tại điểm đó. Nó cho biết hàm số đang tăng lên, giảm xuống hay đứng yên tại điểm đang xét.

Hình dung đơn giản, nếu bạn đang lái xe, đạo hàm sẽ cho biết vận tốc của bạn tại một thời điểm cụ thể. Nếu vận tốc dương, bạn đang tăng tốc; nếu vận tốc âm, bạn đang giảm tốc; và nếu vận tốc bằng 0, bạn đang giữ nguyên tốc độ.

Về mặt hình học, đạo hàm của một hàm số tại một điểm là hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm đó.

Ký hiệu đạo hàm của hàm số f(x) thường được viết là f'(x), dy/dx, hoặc df/dx.

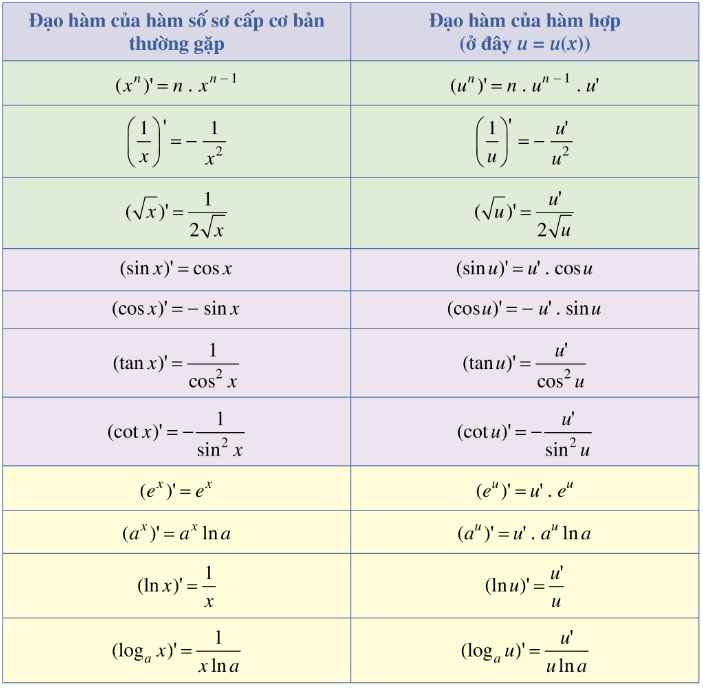
Công thức đạo hàm
Công thức đạo hàm

2. Các Công Thức Đạo Hàm Cơ Bản

Để tính đạo hàm một cách hiệu quả, chúng ta cần nắm vững các công thức cơ bản. Dưới đây là danh sách các công thức đạo hàm quan trọng mà bạn cần biết:

  1. Đạo hàm của hằng số: Nếu f(x) = c (với c là hằng số), thì f'(x) = 0. Ví dụ: Nếu f(x) = 5, thì f'(x) = 0.
  2. Đạo hàm của hàm lũy thừa: Nếu f(x) = xn (với n là số thực), thì f'(x) = n * xn-1. Ví dụ: Nếu f(x) = x3, thì f'(x) = 3x2.
  3. Đạo hàm của hàm số mũ: Nếu f(x) = ax (với a > 0 và a ≠ 1), thì f'(x) = ax * ln(a). Ví dụ: Nếu f(x) = 2x, thì f'(x) = 2x * ln(2). Đặc biệt, nếu f(x) = ex, thì f'(x) = ex.
  4. Đạo hàm của hàm logarit: Nếu f(x) = loga(x) (với a > 0 và a ≠ 1), thì f'(x) = 1 / (x * ln(a)). Ví dụ: Nếu f(x) = log2(x), thì f'(x) = 1 / (x * ln(2)). Đặc biệt, nếu f(x) = ln(x), thì f'(x) = 1/x.
  5. Đạo hàm của hàm sin: Nếu f(x) = sin(x), thì f'(x) = cos(x).
  6. Đạo hàm của hàm cos: Nếu f(x) = cos(x), thì f'(x) = -sin(x).
  7. Đạo hàm của hàm tan: Nếu f(x) = tan(x), thì f'(x) = 1 / cos2(x) = sec2(x).
  8. Đạo hàm của hàm cot: Nếu f(x) = cot(x), thì f'(x) = -1 / sin2(x) = -csc2(x).

3. Các Quy Tắc Tính Đạo Hàm

Ngoài các công thức cơ bản, chúng ta cũng cần nắm vững các quy tắc để tính đạo hàm của các hàm số phức tạp hơn:

  • Quy tắc tổng/hiệu: Nếu f(x) = u(x) ± v(x), thì f'(x) = u'(x) ± v'(x).
  • Quy tắc tích: Nếu f(x) = u(x) * v(x), thì f'(x) = u'(x) * v(x) + u(x) * v'(x).
  • Quy tắc thương: Nếu f(x) = u(x) / v(x), thì f'(x) = (u'(x) * v(x) – u(x) * v'(x)) / v(x)2.
  • Quy tắc hàm hợp (Quy tắc dây chuyền): Nếu f(x) = g(h(x)), thì f'(x) = g'(h(x)) * h'(x). Đây là một trong những quy tắc quan trọng nhất và thường được sử dụng để tính đạo hàm của các hàm số phức tạp.

4. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách áp dụng các công thức và quy tắc, chúng ta hãy cùng xem xét một vài ví dụ:

Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x4 + 2x2 – 5x + 7.

Giải:

f'(x) = (3x4)’ + (2x2)’ – (5x)’ + (7)’

f'(x) = 3 * 4x3 + 2 * 2x – 5 + 0

f'(x) = 12x3 + 4x – 5

Ví dụ 2: Tính đạo hàm của hàm số f(x) = sin(x) * cos(x).

Giải:

Áp dụng quy tắc tích: f'(x) = (sin(x))’ * cos(x) + sin(x) * (cos(x))’

f'(x) = cos(x) * cos(x) + sin(x) * (-sin(x))

f'(x) = cos2(x) – sin2(x)

f'(x) = cos(2x)

Ví dụ 3: Tính đạo hàm của hàm số f(x) = ln(x2 + 1).

Giải:

Áp dụng quy tắc hàm hợp: f'(x) = (ln(u))’ * u’, với u = x2 + 1.

f'(x) = (1/u) * (2x)

f'(x) = 2x / (x2 + 1)

5. Bài Tập Thực Hành

Để củng cố kiến thức, hãy thử giải các bài tập sau:

  1. Tính đạo hàm của hàm số f(x) = 5x3 – 4x + 2.
  2. Tính đạo hàm của hàm số f(x) = ex * sin(x).
  3. Tính đạo hàm của hàm số f(x) = (x + 1) / (x – 1).
  4. Tính đạo hàm của hàm số f(x) = √(x2 + 4).
  5. Tính đạo hàm của hàm số f(x) = tan(2x).

6. Ứng Dụng Của Đạo Hàm

**Đạo hàm** không chỉ là một khái niệm trừu tượng trong Toán học mà còn có rất nhiều ứng dụng thực tế trong cuộc sống. Một số ứng dụng tiêu biểu bao gồm:

  • Tìm cực trị của hàm số: Đạo hàm giúp chúng ta xác định các điểm cực đại và cực tiểu của một hàm số, từ đó giải quyết các bài toán tối ưu hóa.
  • Xác định tính đơn điệu của hàm số: Đạo hàm cho biết hàm số đang tăng hay giảm trên một khoảng nào đó.
  • Tính vận tốc và gia tốc: Trong vật lý, đạo hàm được sử dụng để tính vận tốc và gia tốc của một vật thể chuyển động.
  • Phân tích kinh tế: Trong kinh tế, đạo hàm được sử dụng để phân tích các khái niệm như chi phí biên, doanh thu biên và lợi nhuận biên.
  • Giải các bài toán liên quan đến tốc độ thay đổi: Ví dụ, tính tốc độ thay đổi của dân số, tốc độ phản ứng hóa học, v.v.

Bạn có thể tìm hiểu thêm về các ứng dụng khác của đạo hàm và các kiến thức Toán học hữu ích khác tại Phan Rang Soft – Chuyên mục Giáo Dục.

7. Kết Luận

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về **công thức đạo hàm** và tầm quan trọng của nó trong Toán học và các lĩnh vực khác. Hãy luyện tập thường xuyên để nắm vững các công thức và quy tắc, từ đó tự tin giải quyết các bài toán phức tạp hơn. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với Phan Rang Soft để được hỗ trợ. Chúc bạn học tập tốt!

Thông tin liên hệ Phan Rang Soft:

Hotline: 0865.427.637

Zalo: https://zalo.me/0865427637

Email: phanrangninhthuansoft@gmail.com

Pinterest: https://in.pinterest.com/phanrangsoftvn/

Facebook: https://www.facebook.com/phanrangsoft/

X: https://x.com/phanrangsoft

Website: https://phanrangsoft.com/