Chưa có sản phẩm trong giỏ hàng.
Chào mừng bạn đến với thế giới toán học thú vị tại Phan Rang Soft! Hôm nay, chúng ta sẽ cùng nhau khám phá một chủ đề tưởng chừng phức tạp nhưng lại vô cùng hấp dẫn: Chu vi elip. Elip là một hình học quan trọng, xuất hiện nhiều trong tự nhiên và ứng dụng kỹ thuật. Việc tính toán chu vi của nó không hề đơn giản như đường tròn, nhưng đừng lo, Phan Rang Soft sẽ giúp bạn hiểu rõ và chinh phục bài toán này!
Tóm tắt nội dung
1. Elip Là Gì?
Trước khi đi sâu vào công thức tính chu vi, hãy cùng ôn lại khái niệm cơ bản về elip. Elip là một đường cong kín, được định nghĩa là tập hợp các điểm sao cho tổng khoảng cách từ mỗi điểm đến hai điểm cố định (gọi là tiêu điểm) là một hằng số. Elip có hai trục đối xứng: trục lớn (dài nhất) và trục nhỏ (ngắn nhất). Nửa độ dài của trục lớn được gọi là bán trục lớn (a), và nửa độ dài của trục nhỏ được gọi là bán trục nhỏ (b).
Hình minh họa Elip:
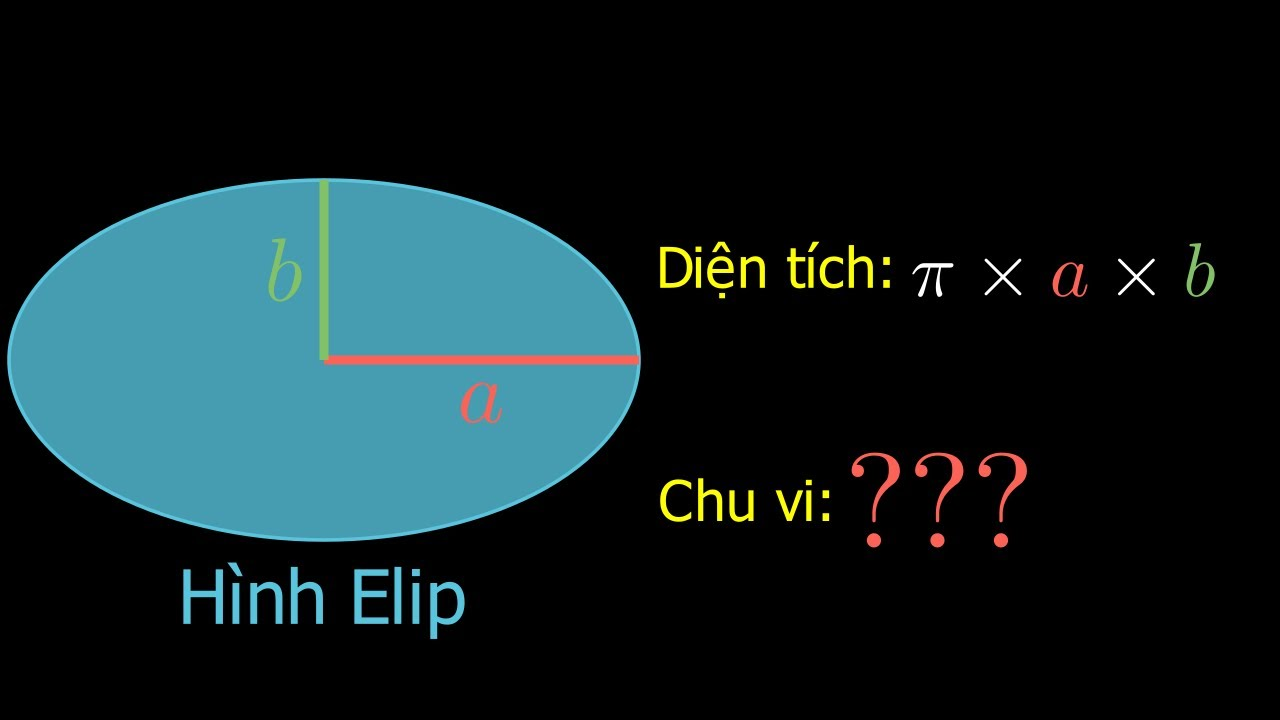
2. Tại Sao Chu Vi Elip Lại Khó Tính?
Khác với đường tròn, chu vi của elip không có công thức đơn giản và chính xác tuyệt đối. Điều này là do đường cong của elip không đồng đều, khiến cho việc tính toán trở nên phức tạp. Chúng ta không thể áp dụng công thức 2πr như với đường tròn. Thay vào đó, chúng ta phải sử dụng các phương pháp xấp xỉ để tìm ra giá trị gần đúng của chu vi elip.
3. Các Phương Pháp Tính Xấp Xỉ Chu Vi Elip
Dưới đây là một số phương pháp phổ biến để tính xấp xỉ chu vi elip:
3.1. Công Thức Ramanujan (Xấp xỉ 1)
Một trong những công thức xấp xỉ nổi tiếng nhất là công thức Ramanujan:
P ≈ π[3(a + b) – √((a + 3b)(3a + b))]
Trong đó:
- P là chu vi elip
- a là bán trục lớn
- b là bán trục nhỏ
Công thức này cho kết quả khá chính xác, đặc biệt khi a và b gần nhau.
3.2. Công Thức Ramanujan (Xấp xỉ 2)
Một công thức khác của Ramanujan, thường cho kết quả chính xác hơn:
P ≈ π(a + b)[1 + (3h / (10 + √(4 – 3h)))]
Trong đó: h = ((a – b) / (a + b))^2
3.3. Công Thức Maclaurin
Công thức Maclaurin sử dụng khai triển chuỗi vô hạn để tính chu vi elip. Công thức này có dạng:
P = 2πa [1 – (1/4)e^2 – (3/64)e^4 – (5/256)e^6 – …]
Trong đó: e là độ lệch tâm của elip, e = √(1 – (b^2 / a^2))
Càng sử dụng nhiều số hạng trong chuỗi, kết quả càng chính xác.
3.4. Sử dụng Tích Phân
Về mặt lý thuyết, chu vi elip có thể được tính bằng tích phân:
P = 4a ∫[0 đến π/2] √(1 – e^2 * sin^2(θ)) dθ
Tuy nhiên, tích phân này là một tích phân elliptic và không có nghiệm giải tích sơ cấp. Do đó, chúng ta cần sử dụng các phương pháp số để tính gần đúng giá trị của nó.
4. Ví Dụ Minh Họa
Giả sử chúng ta có một elip với bán trục lớn a = 5 và bán trục nhỏ b = 3. Hãy tính xấp xỉ chu vi elip bằng công thức Ramanujan (xấp xỉ 1):
P ≈ π[3(5 + 3) – √((5 + 3*3)(3*5 + 3))]
P ≈ π[24 – √(14 * 18)]
P ≈ π[24 – √252]
P ≈ π[24 – 15.87]
P ≈ π * 8.13
P ≈ 25.54
Vậy, chu vi elip xấp xỉ bằng 25.54 đơn vị.
5. Ứng Dụng Thực Tế của Chu Vi Elip
Việc tính toán chu vi elip có nhiều ứng dụng trong thực tế, bao gồm:
- Thiết kế: Trong thiết kế kiến trúc và kỹ thuật, elip được sử dụng để tạo ra các hình dạng đẹp mắt và hiệu quả. Việc tính toán chu vi elip giúp xác định lượng vật liệu cần thiết.
- Thiên văn học: Quỹ đạo của các hành tinh quanh Mặt Trời là hình elip. Việc tính toán chu vi elip giúp ước tính khoảng đường mà hành tinh di chuyển trong một khoảng thời gian nhất định.
- Quang học: Elip được sử dụng trong thiết kế các loại thấu kính và gương, đặc biệt trong các hệ thống quang học đòi hỏi độ chính xác cao.
- Toán học và Vật lý: Các bài toán liên quan đến chu vi elip giúp củng cố kiến thức về tích phân, chuỗi số và các phương pháp xấp xỉ.
6. Bài Tập Luyện Tập
Hãy thử sức với các bài tập sau để củng cố kiến thức:
- Bài 1: Tính xấp xỉ chu vi elip với a = 8 và b = 6 bằng cả hai công thức Ramanujan. So sánh kết quả.
- Bài 2: Tìm độ lệch tâm của một elip có a = 10 và b = 4.
- Bài 3: Nghiên cứu và so sánh độ chính xác của các phương pháp tính xấp xỉ chu vi elip khác nhau.
7. Phan Rang Soft – Nơi Khơi Nguồn Đam Mê Toán Học
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về chu vi elip và các phương pháp tính toán liên quan. Toán học không hề khô khan như bạn nghĩ, mà ẩn chứa vô vàn điều thú vị đang chờ bạn khám phá. Để tìm hiểu thêm nhiều kiến thức bổ ích khác, hãy truy cập chuyên mục Giáo dục của Phan Rang Soft. Tại đây, bạn sẽ tìm thấy nhiều bài viết chất lượng về toán học, khoa học và các lĩnh vực khác. Chúng tôi luôn nỗ lực mang đến những nội dung dễ hiểu, hấp dẫn và hữu ích nhất cho độc giả.
Phan Rang Soft không chỉ là một trang web cung cấp kiến thức, mà còn là một cộng đồng đam mê học hỏi. Chúng tôi khuyến khích bạn chia sẻ ý kiến, đặt câu hỏi và tham gia thảo luận để cùng nhau tiến bộ. Hãy để Phan Rang Soft trở thành người bạn đồng hành trên con đường chinh phục tri thức!
Bạn muốn tìm hiểu thêm về lập trình, thiết kế web hoặc các lĩnh vực công nghệ khác? Đừng ngần ngại truy cập website chính thức của chúng tôi: https://phanrangsoft.com/
Kết luận
Hi vọng qua bài viết này, bạn đã có cái nhìn tổng quan và sâu sắc hơn về chu vi elip, từ định nghĩa, công thức tính, ứng dụng thực tế đến các bài tập luyện tập. Toán học luôn là một phần quan trọng trong cuộc sống, giúp chúng ta phát triển tư duy logic và khả năng giải quyết vấn đề. Đừng ngại khám phá và thử thách bản thân, bạn sẽ thấy toán học thú vị hơn bạn nghĩ!
Cảm ơn bạn đã đọc bài viết. Mọi thắc mắc xin vui lòng liên hệ:
Hotline: 0865.427.637
Zalo: https://zalo.me/0865427637
Email: phanrangninhthuansoft@gmail.com
Pinterest: https://in.pinterest.com/phanrangsoftvn/
Facebook: https://www.facebook.com/phanrangsoft/
Website: https://phanrangsoft.com/
