Blog, Giáo dục

Công thức đạo hàm sơ cấp, cấp cao, lượng giác đầy đủ – Cách tính và ứng dụng đầy đủ

Posted on by vantuongthang

Chào mừng bạn đến với thế giới đạo hàm! Đạo hàm là một công cụ toán học mạnh mẽ, được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Bài viết này, được biên soạn bởi Phan Rang Soft, sẽ cung cấp cho bạn một cái nhìn toàn diện về công thức đạo hàm sơ cấp, cấp cao và lượng giác, đi kèm với các ví dụ minh họa, bài tập thực hành và ứng dụng thực tế. Hãy cùng khám phá!

1. Đạo Hàm Sơ Cấp: Nền Tảng Vững Chắc

Trước khi đi sâu vào các công thức phức tạp, hãy cùng nhau ôn lại những công thức đạo hàm sơ cấp quan trọng nhất. Đây là những viên gạch đầu tiên để bạn xây dựng kiến thức vững chắc về đạo hàm.

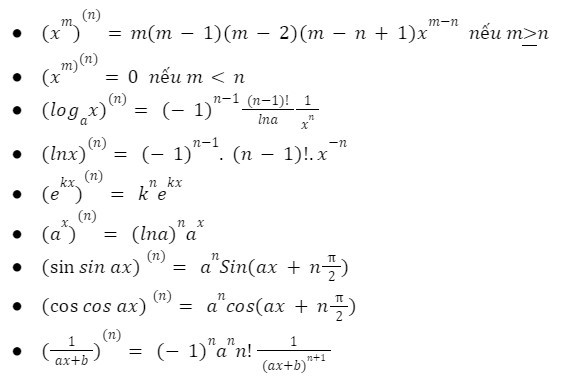
Công thức đạo hàm sơ cấp, cấp cao, lượng giác đầy đủ
Công thức đạo hàm sơ cấp, cấp cao, lượng giác đầy đủ

1.1. Các Quy Tắc Đạo Hàm Cơ Bản:

Các quy tắc này giúp bạn đơn giản hóa quá trình tính đạo hàm của các hàm số phức tạp.

  1. Đạo hàm của hằng số: (c)’ = 0, với c là hằng số.
  2. Đạo hàm của lũy thừa: (xn)’ = n*xn-1, với n là số thực.
  3. Đạo hàm của tổng/hiệu: (u ± v)’ = u’ ± v’
  4. Đạo hàm của tích: (u*v)’ = u’*v + u*v’
  5. Đạo hàm của thương: (u/v)’ = (u’*v – u*v’) / v2, với v ≠ 0.
  6. Đạo hàm của hàm hợp: (f(g(x)))’ = f'(g(x))*g'(x) (Quy tắc chuỗi)

1.2. Bảng Đạo Hàm Các Hàm Số Thường Gặp:

Ghi nhớ bảng đạo hàm này sẽ giúp bạn tiết kiệm thời gian và tránh sai sót khi giải bài tập.

  • (x)’ = 1
  • (ex)’ = ex
  • (ln(x))’ = 1/x, với x > 0
  • (ax)’ = ax * ln(a), với a > 0, a ≠ 1
  • (loga(x))’ = 1 / (x * ln(a)), với a > 0, a ≠ 1, x > 0

1.3. Ví dụ Minh Họa:

Hãy cùng xem một vài ví dụ để hiểu rõ hơn cách áp dụng các quy tắc và công thức trên:

Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x – 5.

Áp dụng quy tắc tổng/hiệu và đạo hàm của lũy thừa, ta có:

f'(x) = (3x2)’ + (2x)’ – (5)’ = 3*(x2)’ + 2*(x)’ – 0 = 3*2x + 2*1 = 6x + 2.

Ví dụ 2: Tính đạo hàm của hàm số g(x) = x*ex.

Áp dụng quy tắc tích, ta có:

g'(x) = (x)’*ex + x*(ex)’ = 1*ex + x*ex = ex(1 + x).

Ví dụ 3: Tính đạo hàm của hàm số h(x) = ln(x2 + 1).

Áp dụng quy tắc chuỗi, ta có:

h'(x) = (ln(x2 + 1))’ = (1 / (x2 + 1)) * (x2 + 1)’ = (1 / (x2 + 1)) * 2x = 2x / (x2 + 1).

2. Đạo Hàm Cấp Cao: Khám Phá Sự Biến Thiên

Đạo hàm cấp cao là đạo hàm của đạo hàm. Đạo hàm cấp hai (f”(x)) cho biết tốc độ thay đổi của đạo hàm cấp nhất, giúp ta xác định độ cong của đồ thị hàm số. Tương tự, đạo hàm cấp ba, cấp bốn,… cung cấp thông tin về sự biến thiên phức tạp hơn của hàm số.

2.1. Công Thức Tính Đạo Hàm Cấp Cao:

Để tính đạo hàm cấp cao, bạn chỉ cần lấy đạo hàm liên tiếp của hàm số ban đầu.

Ví dụ:

  • f'(x) là đạo hàm cấp nhất.
  • f”(x) = (f'(x))’ là đạo hàm cấp hai.
  • f”'(x) = (f”(x))’ là đạo hàm cấp ba.
  • …
  • f(n)(x) = (f(n-1)(x))’ là đạo hàm cấp n.

2.2. Ví dụ Minh Họa:

Ví dụ: Tính đạo hàm cấp hai của hàm số f(x) = x3 – 4x2 + 5x – 2.

Đầu tiên, tính đạo hàm cấp nhất:

f'(x) = 3x2 – 8x + 5.

Tiếp theo, tính đạo hàm cấp hai:

f”(x) = (3x2 – 8x + 5)’ = 6x – 8.

2.3. Ứng Dụng của Đạo Hàm Cấp Cao:

Đạo hàm cấp cao được sử dụng rộng rãi trong:

  • Vật lý: Tính gia tốc, vận tốc giật.
  • Kinh tế: Phân tích sự thay đổi của lợi nhuận, chi phí.
  • Toán học: Nghiên cứu tính lồi lõm của đồ thị hàm số, tìm điểm uốn.

Bạn có thể tìm hiểu thêm nhiều kiến thức bổ ích khác về toán học tại Phan Rang Soft – Giáo Dục.

3. Đạo Hàm Lượng Giác: Chinh Phục Hàm Sin, Cos, Tan…

Đạo hàm lượng giác là đạo hàm của các hàm số lượng giác như sin(x), cos(x), tan(x), cot(x), sec(x), csc(x). Chúng đóng vai trò quan trọng trong việc mô tả các hiện tượng dao động và tuần hoàn.

3.1. Bảng Đạo Hàm Các Hàm Số Lượng Giác:

Hãy nắm vững bảng đạo hàm này để giải quyết các bài toán liên quan đến hàm số lượng giác:

  • (sin(x))’ = cos(x)
  • (cos(x))’ = -sin(x)
  • (tan(x))’ = 1/cos2(x) = sec2(x) = 1 + tan2(x)
  • (cot(x))’ = -1/sin2(x) = -csc2(x) = -(1 + cot2(x))
  • (sec(x))’ = sec(x)*tan(x)
  • (csc(x))’ = -csc(x)*cot(x)

3.2. Ví dụ Minh Họa:

Ví dụ 1: Tính đạo hàm của hàm số f(x) = sin(2x).

Áp dụng quy tắc chuỗi, ta có:

f'(x) = (sin(2x))’ = cos(2x) * (2x)’ = cos(2x) * 2 = 2cos(2x).

Ví dụ 2: Tính đạo hàm của hàm số g(x) = tan(x2 + 1).

Áp dụng quy tắc chuỗi, ta có:

g'(x) = (tan(x2 + 1))’ = sec2(x2 + 1) * (x2 + 1)’ = sec2(x2 + 1) * 2x = 2x*sec2(x2 + 1).

3.3. Ứng Dụng của Đạo Hàm Lượng Giác:

Đạo hàm lượng giác được sử dụng rộng rãi trong:

  • Vật lý: Mô tả dao động điều hòa, sóng điện từ.
  • Kỹ thuật: Phân tích mạch điện xoay chiều, thiết kế hệ thống điều khiển.
  • Toán học: Giải các bài toán liên quan đến tích phân, phương trình vi phân.

4. Bài Tập Thực Hành:

Để củng cố kiến thức, hãy thử sức với các bài tập sau:

  1. Tính đạo hàm của hàm số f(x) = x4 – 3x2 + 7x – 1.
  2. Tính đạo hàm của hàm số g(x) = (x2 + 1) / (x – 1).
  3. Tính đạo hàm của hàm số h(x) = esin(x).
  4. Tính đạo hàm cấp hai của hàm số k(x) = x3 + 2x2 – 5x + 3.
  5. Tính đạo hàm của hàm số l(x) = cos(3x) + sin(x/2).

5. Kết luận:

Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về công thức đạo hàm sơ cấp, cấp cao và lượng giác. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành thạo vào giải quyết các bài toán thực tế. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với Phan Rang Soft để được hỗ trợ!

Thông tin liên hệ:

Hotline: 0865.427.637

Zalo: https://zalo.me/0865427637

Email: phanrangninhthuansoft@gmail.com

Pinterest: https://in.pinterest.com/phanrangsoftvn/

Facebook: https://www.facebook.com/phanrangsoft/

X: https://x.com/phanrangsoft

Website: https://phanrangsoft.com/