Bất đẳng thức Bunhiacopxki - Đầy đủ, chi tiết

Chào mừng bạn đến với thế giới toán học đầy thú vị! Hôm nay, chúng ta sẽ cùng nhau khám phá một công cụ mạnh mẽ và vô cùng hữu ích trong giải toán, đó chính là Bất đẳng thức Bunhiacopxki. Đây không chỉ là một công thức khô khan, mà là một chìa khóa giúp bạn giải quyết nhiều bài toán hóc búa một cách dễ dàng và hiệu quả hơn. Cùng Phan Rang Soft tìm hiểu sâu hơn về bất đẳng thức này nhé!

Tóm tắt nội dung

1. Giới thiệu về Bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki, hay còn được gọi là Cauchy-Schwarz, là một trong những bất đẳng thức quan trọng nhất trong toán học. Nó được đặt theo tên của hai nhà toán học Viktor Yakovlevich Bunyakovsky và Hermann Amandus Schwarz. Bất đẳng thức này có nhiều ứng dụng trong các lĩnh vực khác nhau, từ giải toán sơ cấp đến các bài toán phức tạp trong giải tích và đại số tuyến tính.

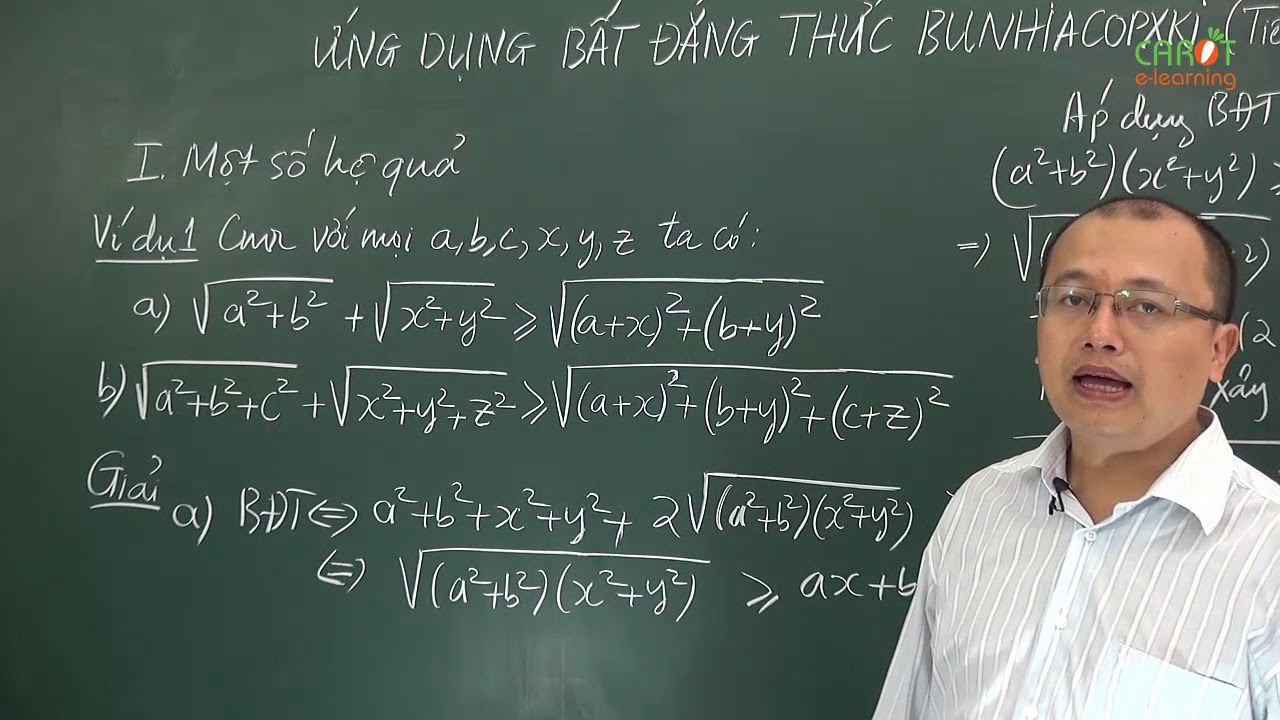
1.1. Phát biểu tổng quát

Cho hai dãy số thực (a₁, a₂, …, a_n) và (b₁, b₂, …, b_n). Khi đó, ta có:

(a₁² + a₂² + … + a_n²)(b₁² + b₂² + … + b_n²) ≥ (a₁b₁ + a₂b₂ + … + a_nb_n)²

Dấu bằng xảy ra khi và chỉ khi hai dãy số tỉ lệ với nhau, tức là tồn tại một số k sao cho a_i = kb_i với mọi i = 1, 2, …, n.

1.2. Các dạng khác của Bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki có nhiều dạng khác nhau, phù hợp với từng bài toán cụ thể. Dưới đây là một số dạng phổ biến:

Dạng tích phân: Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a, b]. Khi đó:(∫_a^b f²(x) dx)(∫_a^b g²(x) dx) ≥ (∫_a^b f(x)g(x) dx)²
Dạng cho vector: Cho hai vector u = (u₁, u₂, …, u_n) và v = (v₁, v₂, …, v_n) trong không gian n chiều. Khi đó:||u||² ||v||² ≥ (u.v)²
Trong đó, ||u|| là độ dài của vector u và u.v là tích vô hướng của hai vector u và v.

2. Chứng minh Bất đẳng thức Bunhiacopxki

Có nhiều cách để chứng minh Bất đẳng thức Bunhiacopxki. Dưới đây là một cách chứng minh phổ biến sử dụng phương pháp đại số:

Xét biểu thức:

S = (a₁x – b₁)² + (a₂x – b₂)² + … + (a_nx – b_n)²

Ta thấy rằng S ≥ 0 với mọi giá trị của x.

Khai triển biểu thức S, ta được:

S = (a₁² + a₂² + … + a_n²)x² – 2(a₁b₁ + a₂b₂ + … + a_nb_n)x + (b₁² + b₂² + … + b_n²)

Đây là một tam thức bậc hai theo biến x. Vì S ≥ 0 với mọi x, nên delta (Δ) của tam thức này phải nhỏ hơn hoặc bằng 0.

Δ = 4(a₁b₁ + a₂b₂ + … + a_nb_n)² – 4(a₁² + a₂² + … + a_n²)(b₁² + b₂² + … + b_n²) ≤ 0

Suy ra:

(a₁b₁ + a₂b₂ + … + a_nb_n)² ≤ (a₁² + a₂² + … + a_n²)(b₁² + b₂² + … + b_n²)

Đây chính là Bất đẳng thức Bunhiacopxki.

3. Ứng dụng của Bất đẳng thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki có rất nhiều ứng dụng trong giải toán. Dưới đây là một số ví dụ minh họa:

3.1. Tìm giá trị lớn nhất và nhỏ nhất

Ví dụ 1: Cho a, b, c là các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức P = √(a + b) + √(b + c) + √(c + a).

Giải:

Áp dụng Bất đẳng thức Bunhiacopxki, ta có:

(1² + 1² + 1²)((√(a + b))² + (√(b + c))² + (√(c + a))²) ≥ (√(a + b) + √(b + c) + √(c + a))²

3(a + b + b + c + c + a) ≥ P²

3(2(a + b + c)) ≥ P²

6 ≥ P²

Suy ra P ≤ √6

Dấu bằng xảy ra khi a = b = c = 1/3.

Vậy giá trị lớn nhất của P là √6.

3.2. Chứng minh bất đẳng thức

Ví dụ 2: Chứng minh rằng với mọi số thực dương a, b, c, ta có:

(a/b) + (b/c) + (c/a) ≥ 3

Giải:

Áp dụng Bất đẳng thức Bunhiacopxki cho hai bộ số (√(a/b), √(b/c), √(c/a)) và (√(b/a), √(c/b), √(a/c)), ta có:

((√(a/b))² + (√(b/c))² + (√(c/a))²)((√(b/a))² + (√(c/b))² + (√(a/c))²) ≥ (√(a/b)*√(b/a) + √(b/c)*√(c/b) + √(c/a)*√(a/c))²

((a/b) + (b/c) + (c/a))((b/a) + (c/b) + (a/c)) ≥ (1 + 1 + 1)² = 9

Áp dụng bất đẳng thức AM-GM (Cô-si) cho hai số dương (a/b) + (b/c) + (c/a) và (b/a) + (c/b) + (a/c), ta có:

((a/b) + (b/c) + (c/a) + (b/a) + (c/b) + (a/c))/2 ≥ √(((a/b) + (b/c) + (c/a))((b/a) + (c/b) + (a/c)))

((a/b) + (b/c) + (c/a) + (b/a) + (c/b) + (a/c))/2 ≥ √9 = 3

(a/b) + (b/c) + (c/a) + (b/a) + (c/b) + (a/c) ≥ 6

Mặt khác, theo bất đẳng thức AM-GM, ta có:

(a/b) + (b/c) + (c/a) ≥ 3∛((a/b)*(b/c)*(c/a)) = 3∛1 = 3

Vậy (a/b) + (b/c) + (c/a) ≥ 3 (điều phải chứng minh).

Xem thêm kiến thức toán học bổ ích tại: https://phanrangsoft.com/category/giao-duc/

4. Bài tập vận dụng

Để củng cố kiến thức về Bất đẳng thức Bunhiacopxki, bạn hãy thử sức với một số bài tập sau:

Cho a, b, c là các số thực dương thỏa mãn a² + b² + c² = 1. Tìm giá trị lớn nhất của biểu thức P = a + 2b + 3c.
Chứng minh rằng với mọi số thực a, b, c, ta có: (a + b + c)² ≤ 3(a² + b² + c²).
Cho x, y, z là các số thực dương thỏa mãn x + y + z = 3. Chứng minh rằng: (x²/y) + (y²/z) + (z²/x) ≥ 3.

5. Lưu ý khi sử dụng Bất đẳng thức Bunhiacopxki

Khi sử dụng Bất đẳng thức Bunhiacopxki, bạn cần lưu ý một số điểm sau:

Xác định rõ hai dãy số hoặc hai hàm số cần áp dụng bất đẳng thức.
Kiểm tra điều kiện dấu bằng xảy ra để xác định giá trị lớn nhất hoặc nhỏ nhất chính xác.
Lựa chọn dạng bất đẳng thức phù hợp với từng bài toán cụ thể.

Hi vọng bài viết này đã giúp bạn hiểu rõ hơn về Bất đẳng thức Bunhiacopxki và cách áp dụng nó trong giải toán. Hãy luyện tập thường xuyên để làm chủ công cụ mạnh mẽ này và đạt được nhiều thành công trong học tập!

Cảm ơn bạn đã theo dõi bài viết của Phan Rang Soft. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.

Thông tin liên hệ:

Hotline: 0865.427.637

Zalo: https://zalo.me/0865427637

Email: phanrangninhthuansoft@gmail.com

Pinterest: https://in.pinterest.com/phanrangsoftvn/

Facebook: https://www.facebook.com/phanrangsoft/

X: https://x.com/phanrangsoft

Website: https://phanrangsoft.com/